Bogdanov-Takens Bifurcation in SIRI Model with Multiple Reinfection of COVID-19
Main Article Content
Abstract
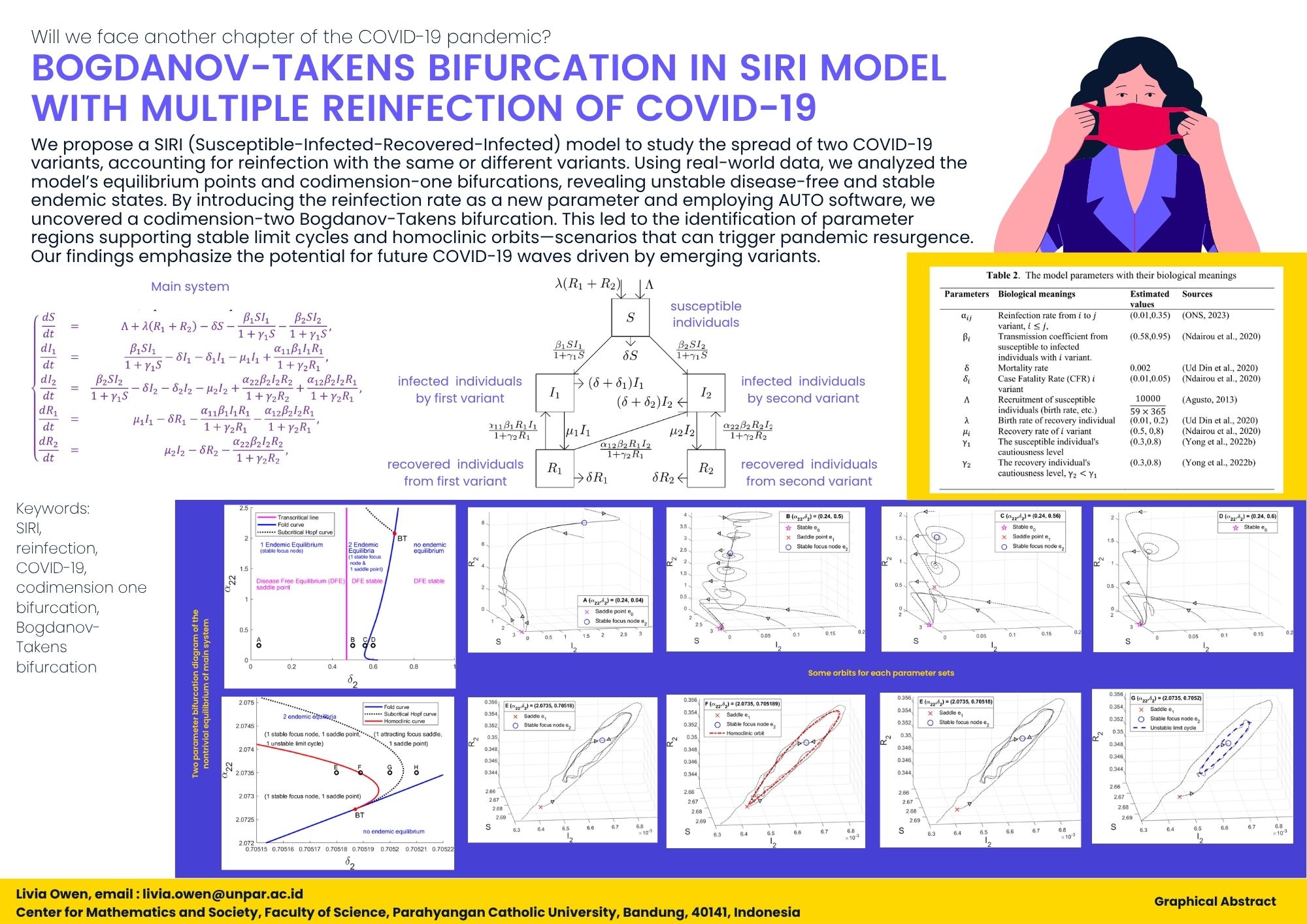
In the presence of cases of COVID-19 reinfection, we propose a SIRI (Susceptible-Infected-Recovery-Infected) spread model of two COVID-19 variants. This model considers the possibility of individuals becoming reinfected with the same or different variants, although the risk of reinfection with the same variant remains lower due to natural immunity from previous infections. Besides analyzing the stability of equilibrium points, we focus on codimension-one bifurcations. Our initial numerical simulations used parameters obtained from real data collected through a British government survey. Our analysis revealed unstable disease-free equilibria and stable endemic equilibria. By varying the Case Fatality Rate parameter, we identified all codimension-one bifurcations. To further investigate the model's dynamics, we introduced a new parameter, the reinfection rate, and utilized AUTO software. Our research led to the discovery of codimension-two bifurcations, specifically the Bogdanov-Takens bifurcation. We identified the parameter domain where a stable limit cycle and homoclinic orbit occur in the presence of the Bogdanov-Takens bifurcation. We also simulated parameter variations that could trigger a pandemic resurgence. This highlights the possibility of emerging variants causing a pandemic return.
Downloads
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Transfer of Copyrights
- In the event of publication of the manuscript entitled [INSERT MANUSCRIPT TITLE AND REF NO.] in the Malaysian Journal of Science, I hereby transfer copyrights of the manuscript title, abstract and contents to the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) for the full legal term of copyright and any renewals thereof throughout the world in any format, and any media for communication.
Conditions of Publication
- I hereby state that this manuscript to be published is an original work, unpublished in any form prior and I have obtained the necessary permission for the reproduction (or am the owner) of any images, illustrations, tables, charts, figures, maps, photographs and other visual materials of whom the copyrights is owned by a third party.
- This manuscript contains no statements that are contradictory to the relevant local and international laws or that infringes on the rights of others.
- I agree to indemnify the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) in the event of any claims that arise in regards to the above conditions and assume full liability on the published manuscript.
Reviewer’s Responsibilities
- Reviewers must treat the manuscripts received for reviewing process as confidential. It must not be shown or discussed with others without the authorization from the editor of MJS.
- Reviewers assigned must not have conflicts of interest with respect to the original work, the authors of the article or the research funding.
- Reviewers should judge or evaluate the manuscripts objective as possible. The feedback from the reviewers should be express clearly with supporting arguments.
- If the assigned reviewer considers themselves not able to complete the review of the manuscript, they must communicate with the editor, so that the manuscript could be sent to another suitable reviewer.
Copyright: Rights of the Author(s)
- Effective 2007, it will become the policy of the Malaysian Journal of Science (published by the Faculty of Science, University of Malaya) to obtain copyrights of all manuscripts published. This is to facilitate:
- Protection against copyright infringement of the manuscript through copyright breaches or piracy.
- Timely handling of reproduction requests from authorized third parties that are addressed directly to the Faculty of Science, University of Malaya.
- As the author, you may publish the fore-mentioned manuscript, whole or any part thereof, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given. You may produce copies of your manuscript, whole or any part thereof, for teaching purposes or to be provided, on individual basis, to fellow researchers.
- You may include the fore-mentioned manuscript, whole or any part thereof, electronically on a secure network at your affiliated institution, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- You may include the fore-mentioned manuscript, whole or any part thereof, on the World Wide Web, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- In the event that your manuscript, whole or any part thereof, has been requested to be reproduced, for any purpose or in any form approved by the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers), you will be informed. It is requested that any changes to your contact details (especially e-mail addresses) are made known.
Copyright: Role and responsibility of the Author(s)
- In the event of the manuscript to be published in the Malaysian Journal of Science contains materials copyrighted to others prior, it is the responsibility of current author(s) to obtain written permission from the copyright owner or owners.
- This written permission should be submitted with the proof-copy of the manuscript to be published in the Malaysian Journal of Science
Licensing Policy
Malaysian Journal of Science is an open-access journal that follows the Creative Commons Attribution-Non-commercial 4.0 International License (CC BY-NC 4.0)
CC BY – NC 4.0: Under this licence, the reusers to distribute, remix, alter, and build upon the content in any media or format for non-commercial purposes only, as long as proper acknowledgement is given to the authors of the original work. Please take the time to read the whole licence agreement (https://creativecommons.org/licenses/by-nc/4.0/legalcode ).
References
Agusto, F. B. (2013). Optimal isolation control strategies and cost-effectiveness analysis of a two-strain avian influenza model. Biosystems, 113(3), 155-164.
Duan, L., Huang, L., & Huang, C. (2021). Spatial dynamics of a diffusive SIRI model with distinct dispersal rates and heterogeneous environment. Communications on Pure and Applied Analysis, 20(10), 3539-3560.
European Centre for Disease Prevention and Control. Available online: https://www.ecdc.europa.eu/en/infectious-disease-topics/z-disease-list/covid-19/ facts/transmission-covid-19 (accessed on Februari 26, 2024).
Martins, J., & Pinto, A. (2017). Bistability of evolutionary stable vaccination strategies in the reinfection SIRI model. Bulletin of mathematical biology, 79, 853-883.
McMahon, A., & Robb, N. C. (2020). Reinfection with SARS-CoV-2: Discrete SIR (susceptible, infected, recovered) modeling using empirical infection data. JMIR public health and surveillance, 6(4), e21168.
Ndaïrou, F., Area, I., Nieto, J. J., & Torres, D. F. (2020). Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos, Solitons & Fractals, 135, 109846.
Nurjanah, A., & Prawoto, B. P. (2022). Dinamika Model Siri Covid-19 Dengan Adanya Pengaruh Kerumunan. MATHunesa: Jurnal Ilmiah Matematika, 10(2), 280-288.
Office for National Statistics (ONS) - Coronavirus (COVID-19) Infection Survey in UK. Available online: https://www.ons.gov.uk/peoplepopulationandcommunity/healthandsocialcare/conditionsanddiseases/datasets/coronaviruscovid19infectionsurveydata (accessed on October 19, 2022).
Our World in Data. SARS-CoV-2 sequences by variant. Available online: https://ourworldindata.org/explorers (accessed on May 2, 2023).
Pinto, L. M., Nanda, V., Sunavala, A., & Rodriques, C. (2021). Reinfection in COVID-19: A scoping review. medical journal armed forces india, 77, S257-S263.
Salman, A. M., Ahmed, I., Mohd, M. H., Jamiluddin, M. S., & Dheyab, M. A. (2021). Scenario analysis of COVID-19 transmission dynamics in Malaysia with the possibility of reinfection and limited medical resources scenarios. Computers in biology and medicine, 133, 104372.
Saxena, S. K. (Ed.). (2020). Coronavirus disease 2019 (COVID-19): epidemiology, pathogenesis, diagnosis, and therapeutics. Springer nature.
Sharma, S., Badshah, V. H., & Gupta, V. K. (2017). Analysis of a SIRI Epidemic Model with Modified Nonlinear Incidence Rateand Latent Period. Asian Journal of Mathematics and Statistics, 10, 1-12.
Strogatz, S. H. (2018). Nonlinear dynamics and chaos with student solutions manual: With applications to physics, biology, chemistry, and engineering. CRC press.
Ud Din, R., Shah, K., Ahmad, I., & Abdeljawad, T. (2020). Study of transmission dynamics of novel COVID-19 by using mathematical model. Advances in Difference Equations, 2020, 1-13.
Van den Driessche, P. (2017). Reproduction numbers of infectious disease models. Infectious disease modelling, 2(3), 288-303.
Wangari, I. M., Sewe, S., Kimathi, G., Wainaina, M., Kitetu, V., & Kaluki, W. (2021). Mathematical modelling of COVID-19 transmission in Kenya: a model with reinfection transmission mechanism. Computational and Mathematical Methods in Medicine, 2021, 1-18.
Wituła, R., & Słota, D. (2010). Cardano's formula, square roots, Chebyshev polynomials and radicals. Journal of Mathematical Analysis and Applications, 363(2), 639-647.
Yale Medicine. Will BA.2.86 ('Pirola'), the New Coronavirus Variant, Increase COVID-19 Cases?. Available online: https://www.yalemedicine.org/news/new-covid-variant-ba286-pirola (accessed on September 1, 2023).
Yang, Y., Zhou, J., & Hsu, C. H. (2019). Threshold dynamics of a diffusive SIRI model with nonlinear incidence rate. Journal of Mathematical Analysis and Applications, 478(2), 874-896.
Yong, B., Owen, L., & Hoseana, J. (2022). Mathematical Analysis of an Epidemic Model for COVID-19. Letters in Biomathematics, 9(1), 3–22.
Yong, B., Hoseana, J., & Owen, L. (2022). A design of governmental policies for the eradication of COVID-19 in Jakarta using an SIR-type mathematical model. Commun. Math. Biol. Neurosci., 2022 (2022), Article ID 26
World Health Organization (WHO). COVID-19 weekly epidemiological update. Available online: https://www.who.int/publications/m/item/weekly-epidemiological-update-on-covid-19 1-september-2023 (accessed on September 1, 2023).